ΣΤ΄ ΤΑΞΗ - ΦΥΣΙΚΗ - ΜΗΧΑΝΙΚΗ
Φ.Ε. 3. Δυνάμεις με επαφή - Δυνάμεις από απόσταση
Α΄. ΔΥΝΑΜΕΙΣ ΜΕ ΕΠΑΦΗ
Όταν ακουμπάμε το σώμα πάνω στο οποίο ασκούμε δύναμη, λέμε πως οι δυνάμεις που ασκούνται είναι σε επαφή.
Η δύναμη που ασκήθηκε πάνω στις λαμαρίες προκάλεσε την μόνιμη παραμόρφωσή τους.
Τα παιδιά, ακουμπώντας την μπάλα, τής ασκούν δύναμη και της προκαλούν αλλαγή κατεύθυνσης της κίνησής της.
|
Η αθλήτρια (Κατερίνα Στεφανίδου) ασκώντας δύναμη πάνω στο κοντάρι, τού προκαλεί μία προσωρινή παραμόρφωση.
Ο χωρικός ασκεί δύναμη μέσω του σκοινιού πάνω στον γάιδαρο και προκαλεί (προσπαθεί τουλάχιστον...) αύξηση της ταχύτητάς του.
|
Β΄. ΔΥΝΑΜΕΙΣ ΑΠΟ ΑΠΟΣΤΑΣΗ
Κάποιες δυνάμεις ασκούνται από απόσταση. Τέτοιες είναι για παράδειγμα οι δυνάμεις που ασκούν και ασκούνται από τους μαγνήτες, η δύναμη με την οποίαν η Γη έλκει όλα τα σώματα που βρίσκονται σ'αυτήν ακόμα κι αν δεν την ακουμπούν (αντικείμενα που κρέμεται από κάπου, δορυφόροι που περιφέρονται γύρω από αυτήν, κλπ.), καθώς και οι βαρυτικές (ελκτικές) δυνάμεις μεταξύ των πλανητών.
Πλησιάστε τους μαγνήτες μεταξύ τους. Βλέπετε πως απωθούνται. Μια αόρατη δύναμη τούς σπρώχνει μακριά.
Πλησιάστε τους μαγνήτες μεταξύ τους. Βλέπετε πως έλκονται. Μια αόρατη δύναμη τούς σπρώχνει τον έναν κοντά στον άλλον.
(Πηγή: www.absorblearning.com)
(Πηγή: www.absorblearning.com)
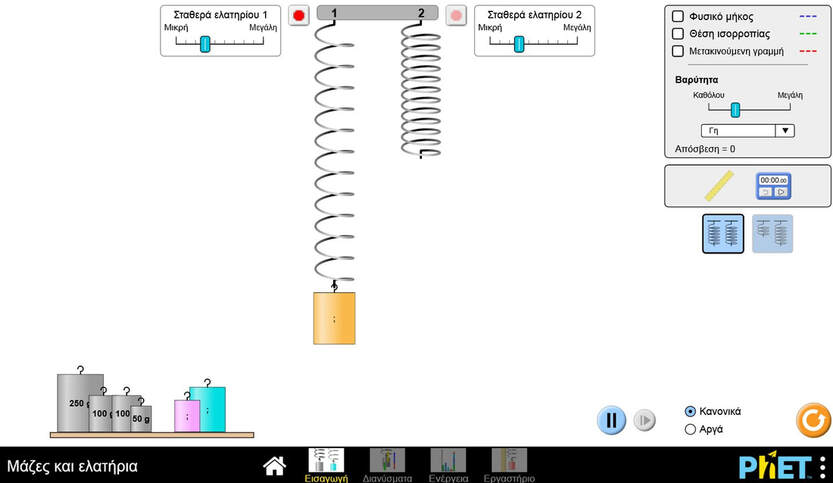
Τα ελατήρια τραβιούνται προς τα κάτω λόγω του βάρους τους, δηλαδή λόγω της δύναμης με την οποίαν τα έλκει η Γη.
Δοκιμάστε το διαδραστικά.
(Παίξτε με την τριβή και την σκληρότητα του ελατηρίου, αν θέλετε. Αν δεν θέλετε πάλι, δεν μας νοιάζει! Ασχοληθείτε μόνο με τα ελατήρια!)
(Πηγή: Πανεπιστήμιο του Κολοράντο)
Δοκιμάστε το διαδραστικά.
(Παίξτε με την τριβή και την σκληρότητα του ελατηρίου, αν θέλετε. Αν δεν θέλετε πάλι, δεν μας νοιάζει! Ασχοληθείτε μόνο με τα ελατήρια!)
(Πηγή: Πανεπιστήμιο του Κολοράντο)
Ο δορυφόρος έλκεται από την Γη
Οι πλανήτες και ο ήλιος είναι ένα θαυμαστό παράδειγμα αμοιβαίας έλξης από απόσταση (από μακριά κι αγαπημένοι, κατά μία έννοια...)
Και... παρεμπιπτόντως:
1. Άλλο μάζα κι άλλο βάρος!
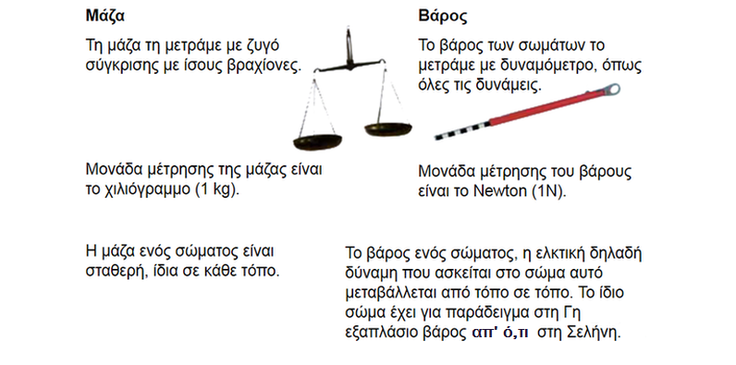
Η μάζα και το βάρος είναι δύο διαφορετικά μεγέθη:
Η μάζα είναι η ποσότητα της ύλης που περιέχεται σε ένα σώμα. Πιο απλά, το άθροισμα των μορίων (όλα τα μόρια, δηλαδή) ενός σώματος αποτελούν την μάζα του.
Την μάζα την μετράμε σε κιλά.
Το πόσο ζυγίζει ένα σώμα, δηλαδή η δύναμη με την οποίαν έλκει το σώμα η Γη, είναι το βάρος του.
Το βάρος το μετράμε σε Newton (Νιούτον) προς τιμήν του Νεύτωνα (ναι, αυτόν, με το μήλο που του έπεσε στο κεφάλι).
Αυτό σημαίνει πως αν ένα υλικό σώμα το πάμε βόλτα σε όλους τους πλανήτες του ηλιακού συστήματος, θα έχει την ίδια μάζα (τον ίδιον αριθμό μορίων) παντού, αλλά διαφορετικό βάρος σε κάθε πλανήτη (επειδή ο καθένας τους, αφού έχει διαφορετικό μέγεθος, θα έλκει το σώμα με διαφορετική δύναμη).
Η μάζα είναι η ποσότητα της ύλης που περιέχεται σε ένα σώμα. Πιο απλά, το άθροισμα των μορίων (όλα τα μόρια, δηλαδή) ενός σώματος αποτελούν την μάζα του.
Την μάζα την μετράμε σε κιλά.
Το πόσο ζυγίζει ένα σώμα, δηλαδή η δύναμη με την οποίαν έλκει το σώμα η Γη, είναι το βάρος του.
Το βάρος το μετράμε σε Newton (Νιούτον) προς τιμήν του Νεύτωνα (ναι, αυτόν, με το μήλο που του έπεσε στο κεφάλι).
Αυτό σημαίνει πως αν ένα υλικό σώμα το πάμε βόλτα σε όλους τους πλανήτες του ηλιακού συστήματος, θα έχει την ίδια μάζα (τον ίδιον αριθμό μορίων) παντού, αλλά διαφορετικό βάρος σε κάθε πλανήτη (επειδή ο καθένας τους, αφού έχει διαφορετικό μέγεθος, θα έλκει το σώμα με διαφορετική δύναμη).
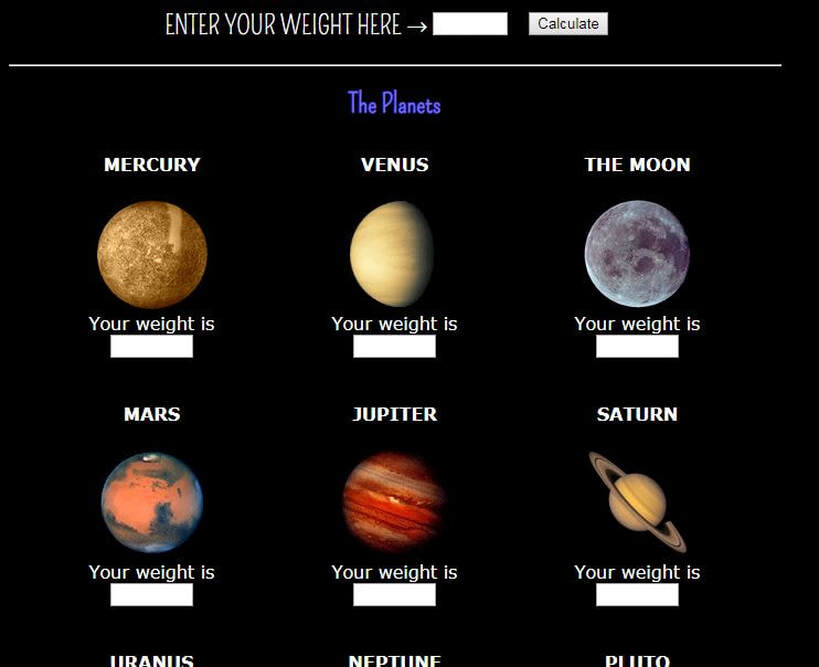
Πόσο ζυγίζουμε σε άλλα ουράνια σώματα;
ΚΛΙΚ στην παρακάτω εικόνα:
Αν θέλετε πιο λεπτομερή αποτελέσματα... πατήστε ΕΔΩ!
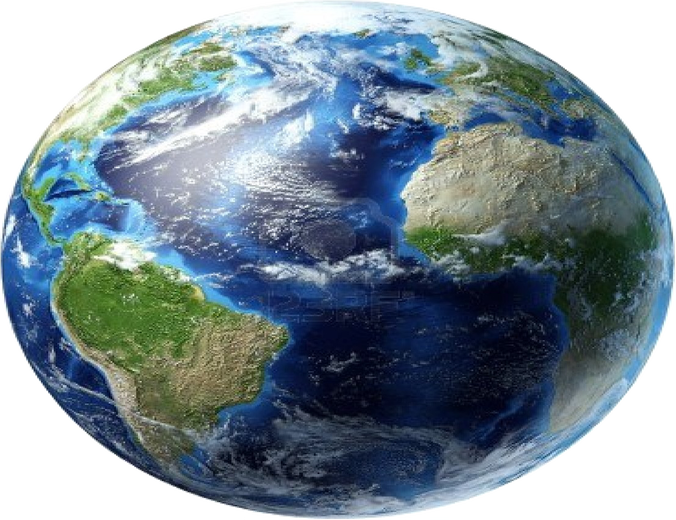
Βέβαια, ούτε στην Γη ζυγίζουμε παντού το ίδιο!
Επειδή ο πλανήτης μας, όπως μάθαμε, είναι πιο πεπλατυσμένος στους πόλους, αυτό σημαίνει πως όταν βρισκόμαστε εκεί θα είμαστε πιο κοντά στο κέντρο της Γης.
Στην πραγματικότητα βέβαια η Γη δεν φαίνεται όπως στην εικόνα από πάνω. Από το διάστημα φαίνεται στρογγυλή. Απλώς, εμείς είμαστε τόσο μικροί σε σχέση με το μέγεθός της, που η ελάχιστη υψομετρική διαφορά μεταξύ πόλων - ισημερινού (περίπου 40 χμ. μεγαλύτερη διάμετρος στον ισημερινό) σ' εμάς φαίνεται πολύ μεγάλη.
Έτσι, αν κάποιος ζυγιστεί στον ισημερινό, η ζυγαριά θα τον δείξει λίγο (πολύ πιο λίγο...) ελαφρύτερον απ' ό,τι αν ζυγιστεί στον Βόρειο ή τον Νότιο πόλο! Με την ίδια λογική, κάποιος άνθρωπος στην κορυφή των Άλπεων θα είναι λίγο ελαφρύτερος απ' ό,τι στην θάλασσα!
Έτσι, αν κάποιος ζυγιστεί στον ισημερινό, η ζυγαριά θα τον δείξει λίγο (πολύ πιο λίγο...) ελαφρύτερον απ' ό,τι αν ζυγιστεί στον Βόρειο ή τον Νότιο πόλο! Με την ίδια λογική, κάποιος άνθρωπος στην κορυφή των Άλπεων θα είναι λίγο ελαφρύτερος απ' ό,τι στην θάλασσα!
Οπότε, πόσο ζυγίζει ένας αστροναύτης;
Ας πούμε ότι βρίσκουμε έναν αστροναύτη στο χωράφι του (που έχει πάει για παράδειγμα να ποτίσει τα καλαμπόκια πριν φύγει για αποστολή στην Σελήνη).
Τον ζυγίζουμε μαζί με την στολή και τον βρίσκουμε... ας πούμε 90 κιλά.
Αν τον στείλουμε στην Σελήνη και τον ξαναζυγίσουμε εκεί, το βάρος του θα είναι πολύ μικρότερο (6 φορές μικρότερο, συγκεκριμένα!), για τον απλό λόγο πως η Σελήνη είναι πολύ μικρότερη από την Γη και άρα έλκει τα σώματα με πολύ μικρότερη δύναμη (6 φορές μικρότερη).
Δηλαδή, ο αστροναύτης στην Σελήνη θα ζυγίζει 90 : 6 = 15 κιλά.
Αν τον στείλουμε στην Σελήνη και τον ξαναζυγίσουμε εκεί, το βάρος του θα είναι πολύ μικρότερο (6 φορές μικρότερο, συγκεκριμένα!), για τον απλό λόγο πως η Σελήνη είναι πολύ μικρότερη από την Γη και άρα έλκει τα σώματα με πολύ μικρότερη δύναμη (6 φορές μικρότερη).
Δηλαδή, ο αστροναύτης στην Σελήνη θα ζυγίζει 90 : 6 = 15 κιλά.
Αν εκτοξεύσουμε το διαστημόπλοιο στο διάστημα, και βγει μια βολτίτσα λίγο έξω για να ξεμουδιάσει και να ξεπιαστεί (είναι και στενάχωρα μέσα στο διαστημόπλοιο...), άραγε πόσο θα ζυγίζει;
Σωστά μαντέψατε!
Αν δεν υπάρχει κοντά του κανένα ουράνιο σώμα για να τον τραβήξει με την ελκτική του δύναμη, στο διάστημα δεν θα ζυγίζει τίποτε!
Δεν θα έχει βάρος!
